Fractals

Fractals are repetitive, self-similar structures, often observed in nature. For a start, look at this somewhat artificial, but simple example.

Fractals always consist of one or several basic elements (in this case the sphere) and a rule how to arrange these elements (in this case: place the new element into the four vortices of the surrounding cube fitting to the old element).

This operation is repeated one more time…

…or here five times.

Structures like these do not look very “natural”. The following branching examples should demonstrate, however, that fractals are everywhere in nature. In the first example, there are two elements (branched and non-branched sticks), which continuously and regularly follow each other. This is the basic structure for fungal colonization in arbuscular mycorrhiza.

The structure looks somewhat more natural, when the branching elements are introduced at random positions.

By playing around with a few parameters familiar structures can be generated.

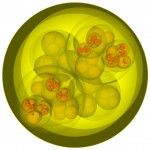
The following fractals are inspired by the alga Volvox. They show spheres within spheres, within spheres… restricted to five levels… First there are four spheres within a single one – a cross-section.

Here with the outer spheres partially transparent.

And here with another look…

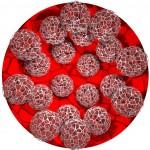
Now, we have got 32 spheres within each sphere.

So much to fractals by now. I surely will come back to this topic.

Further reading:

Fractal Recursions

Fractal Foundation

50 Breathtaking Examples of Fractal Artworks

The World Loses Its Great Fractal Mind, Benoit Mandelbrot, at 85

Generate Beautiful 3D Fractal Images