The golden angle is created by applying the golden ratio to the circumference of a circle. (The ratio of the two arcs defined by this angle is the same as the ratio between the larger arc and the full circle.) This angle is about 137.5 degrees.
- Golden angle
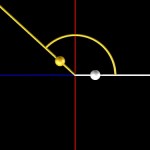
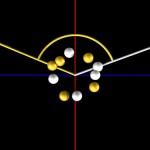
Positioning of many plants organ is directed by this angle as demonstrated below. First let us assume, we apply this angle for positioning balls with alternating colors and gradually increasing radius around the origin. Here comes the third ball in the arrangement shown above…
- Golden angle, three balls
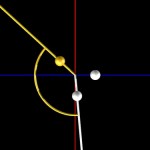
… this is the fourth ball then…
- Golden angle, four balls
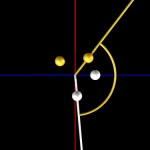
… this is the fifth ball…
- Golden angle, five balls
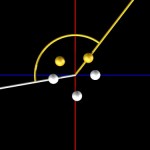
… here comes the tenth ball…
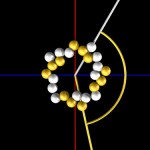
… here the 25th …
- Golden angle, 25 balls
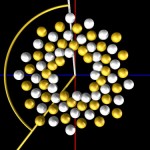
… and here the 75th.
Elements arranged this way can be organized into several spirals (Fermat’s spirals), with the numbers of such spirals being defined by Fibonacci numbers.
- Fermat’s spirals
Here are some crude examples, how such a patterning can be used to model plant structures: First a cactus or a sunflower,…
… then a Christmas tree …
- Conifer-like distribution
… and finally an ordinary shoot with the positions for ramifications.
- Shoot-like distribution
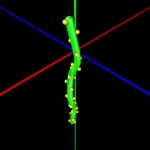
I became interested in the golden angle, because I was impressed by Aeonium plants I saw in Madeira and I wanted to model these plants. So here comes my approach: First I constructed the shortened shoot of such plants by applying the golden angle as indicated above.
- Aeonium shoot
Then I added branches to this shoot.
- Aeonium branches
And finally the branches were used as the starting points of leaves. Some of the parameters of these leaves (inclination, size, form) are gradually changed in this model.
Further reading:
Applying the Golden Ratio to Web Layouts and Objects






Pingback: Nikon COOLPIX L100 Digital Camera - Nikon N6006 - Nikon N6006