Science – a picture story

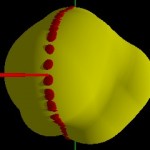
While the visualization approaches discussed for snail-like structures so far only allow to visualize snails produced from bodies of a certain (sphere-like) geometry, here I try to introduce a method suitable for almost any geometry. Let us start with a yellow blob of a random geometry, which is surrounded (in the x-y-plane) by a belt of closely attached disks.

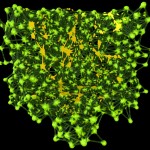
We can produce more of these spheres and combine them into a blob:

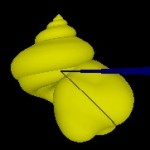
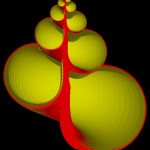
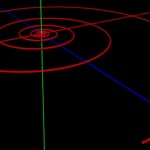
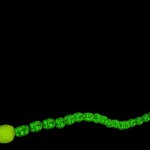
The yellow blob can be swept along a logarithmic spiral (and scaled accordingly) this way producing a snail-like structure.

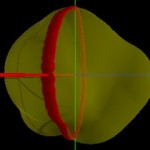
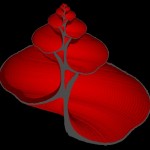
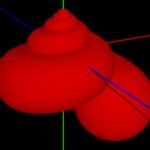
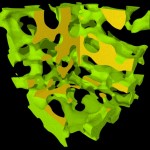
To visualize the shell structure of such a body, the red blob-ring is swept along this path and also scaled accordingly.

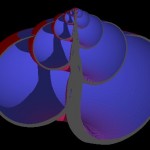
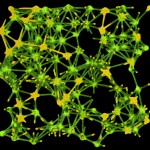
We still have to avoid overlapping structures (which is not too difficult) and we have a nice shell structure.

This principle can be used for bodies of various geometry.

Building a shell VI

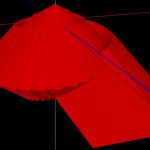
As demonstrated by the artifacts in the upper part of this picture, the approach is not perfect yet. Eventually I will have to improve this.

While the outside of the snails presented so far looks more or less satisfactory, the inside does not. There are problems in particular, when individual turns of the snail are overlapping (as they often are). Here is a first, rough solution to this problem using subsequent (partial) circular arches to construct snails with overlapping turns.

Unfortunately it turned out to be quite difficult to get such constructions any smoother, so I turned to a more thorough approach, constructing snails from small disks (arranged in the right way) combined to a blob. To demonstrate this approach first the individual disks are given.

The produce a solid snail, these disks are enlarged and combined into a blob.

Blob shell

Using two layers of such disks (an internal and an external), it is possible to produce a snail with different textures on the inside and the outside.

Within certain limits it is possible to change the geometry of such snails.

Flat snail

Here comes the limit to this approach. Changing the geometry of the turns themselves leads to problems. Still the structures look nice, but certainly not state of the art… (To be continued…)

Almost any object can be used for rotating on the path of a logarithmic spiral. I start this example with a cube in two orientations. First with each cube separated by 10 degrees.

When each cube is separated by only 1 degree, the resulting structures appear pretty smooth.

While these structures do not look very natural, here are some more natural shells formed from distorted spheres.

When using blobs for constructing such structures, it is possible to decorate the outside with various details: